Es ist mal wieder Zeit für ein bisschen Fußball. Aktuell ist der dritte Spieltag der Europameisterschaft der Männer; heute abend „kämpft“ das deutsche Team um den Einzug ins Achtelfinale – allerdings reicht schon ein 0:1 zum Weiterkommen (als Gruppendritter). Das erste Turnier, das ich bewusst miterlebt habe – allerdings eigentlich erst ab dem Achtelfinale – war die WM 1994 in den USA. Das war auch das bisher letzte Männerturnier mit sechs Vierergruppen, und damals gab es gleich zwei Gruppen, in denen die drittbeste Mannschaft 2 Siege geschafft hat. Gleichzeitig gab es eine Gruppe, in der alle Mannschaften gleich viele Punkte hatten.
Die aktuelle Meisterschaft hat wieder sechs Vierergruppen mit anschließendem Achtelfinale, sodass wieder vier der sechs Dritten weiterkommen können. Der deutsche Bundestrainer, Jogi Löw, lamentierte vor ein paar Tagen über dieses System, dass „manche Mannschaften, die nach dem zweiten Spieltag einen Punkt haben, […] noch immer eine Chance auf das Achtelfinale [haben]“. Nun teile ich Löw’s Kritik an dem System – ich finde auch, dass das Weiterkommen aus einer Gruppe nur an den Ergebnissen aus dieser Gruppe hängen sollte, und dass nicht 24 von 55 Mitgliedern der UEFA ihre Auswahlen zur EM schicken sollten/müssen und dass nicht 16 der 55 Mitgliedsverbände in die K.O.-Runde kommen müssen – aber auch bei einem System, in dem nur die ersten Beiden weiterkommen, gibt es mögliche Konstellationen, in denen ein Team mit 0 Punkten nach zwei Spielen noch Hoffnung haben kann. Das wäre das Gegenteil der Gruppen, in denen der Dritte 6 Punkte hat (wie eben bei der WM 1994: Ein Team verliert alle Spiele, und die übrigen drei Teams gewinnen gegeneinander jeweils ein Spiel: Ergibt 6, 6, 6 und 0 Punkte), nämlich dass ein Team alles gewinnt und die anderen drei gegeneinander jeweils ein Spiel gewinnen, sodass das Ergebnis 9, 3, 3 und 3 Punkte ist.
Das war für mich Stein des Anstoßes, mal die Wikipedia-Artikel zu allen Fußballwelt- und -europameisterschaften zu durchforsten und zu zählen, wie oft solche „bizarren“ Konstellationen auftauchen. (Und die anderen Konstellationen habe ich selbstverständlich auch gezählt.) Rausgekommen ist folgende Tabelle:
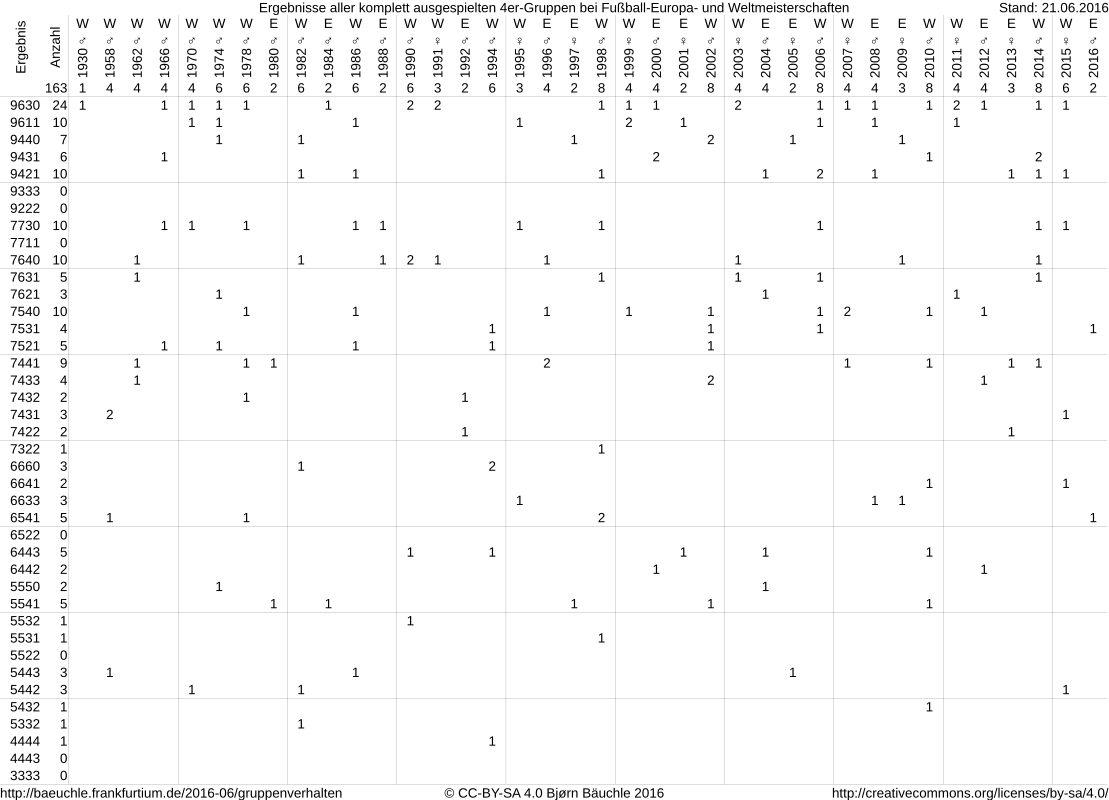
Dabei sind die Vierergruppen von 1954 nicht enthalten, weil diese damals nicht komplett ausgespielt wurden, aber dafür in 1974 und 1978 die Vor- und Zwischenrunde. Die häufigste Konstellation ist die mit der klarsten Hackordnung: Der Beste gewinnt alles, der zweitbeste gewinnt gegen die beiden schlechteren, und der letzte verliert alles. Es sind noch nie alle 6 Spiele Unentschieden ausgegangen (das wäre die letzte Zeile).
Aus den gleichen Daten habe ich ausgelesen, wie oft ein Gruppenerster eigentlich 9, 7, 6, 5, 4 oder 3 Punkte hatte, und entsprechend für die anderen Platzierungen:
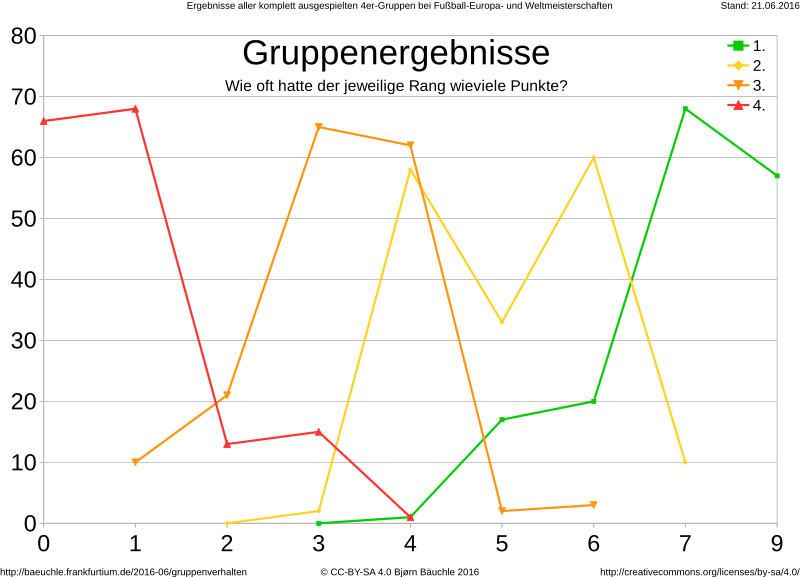
Das häufigste Ergebnis für den Gruppensieger sind also 7 Punkte, für den Gruppenzweiten 6 oder 4, für den Dritten 3 oder 4, und für den letzten 0 oder 1 Punkte. Aber, und das finde ich wichtig, die (historische!) Wahrscheinlichkeit für einen Gruppendritten mit einem Punkt (der Vierte hätte dabei übrigens auch einen Punkt) ist 10/165. Das kann zum Weiterkommen reichen, wenn das Gleiche in zwei anderen Gruppen vorkommt, sodass es zwei Gruppendritte mit einem Punkt gibt, deren Torverhältnis schlechter ist. Die Wahrscheinlichkeit dafür ist (10/165)³, oder etwa 0,02%. Umgekehrt ist die Wahrscheinlichkeit dafür, dass eine Mannschaft als Gruppendritter 5 oder 6 Punkte hat, 3%; diese würden in dem System, wo nur die ersten beiden weiterkommen, rausfliegen. (Von den 5 Mannschaften mit diesem Schicksal sind Schottland 1974, Algerien 1982 und Italien 2004 rausgeflogen, während Argentinien und Belgien 1994 von dem Modus profitiert haben.)
Ich rede dabei von ‚historischer‘ Wahrscheinlichkeit, weil das natürlich davon ausgeht, dass die Gruppenergebnisse heute genauso wahrscheinlich sind wie vor 86 Jahren. Das kann zwar durchaus sein, die Datenbasis ist aber zu klein, um das wirklich sagen zu können. Sehr große Qualitätsunterschiede zwischen den Mannschaften würden zum Beispiel Gruppen mit 9 Punkten für den Ersten und/oder 0 Punkten für den Letzten bevorzugen.